Finding Modes Using Kernel Density Estimates

TL; DR

If you have a unimodal distribution of values, you can use R’s density or Scipy’s gaussian_kde to create density estimates of the data, and then take the maxima of the density estimate to get the mode. See below for actual examples in R and Python.

Mode in R

First, lets do this in R. Need some values to work with.

library(ggplot2)
set.seed(1234)
n_point <- 1000
data_df <- data.frame(values = rnorm(n_point))

ggplot(data_df, aes(x = values)) + geom_histogram()

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

ggplot(data_df, aes(x = values)) + geom_density()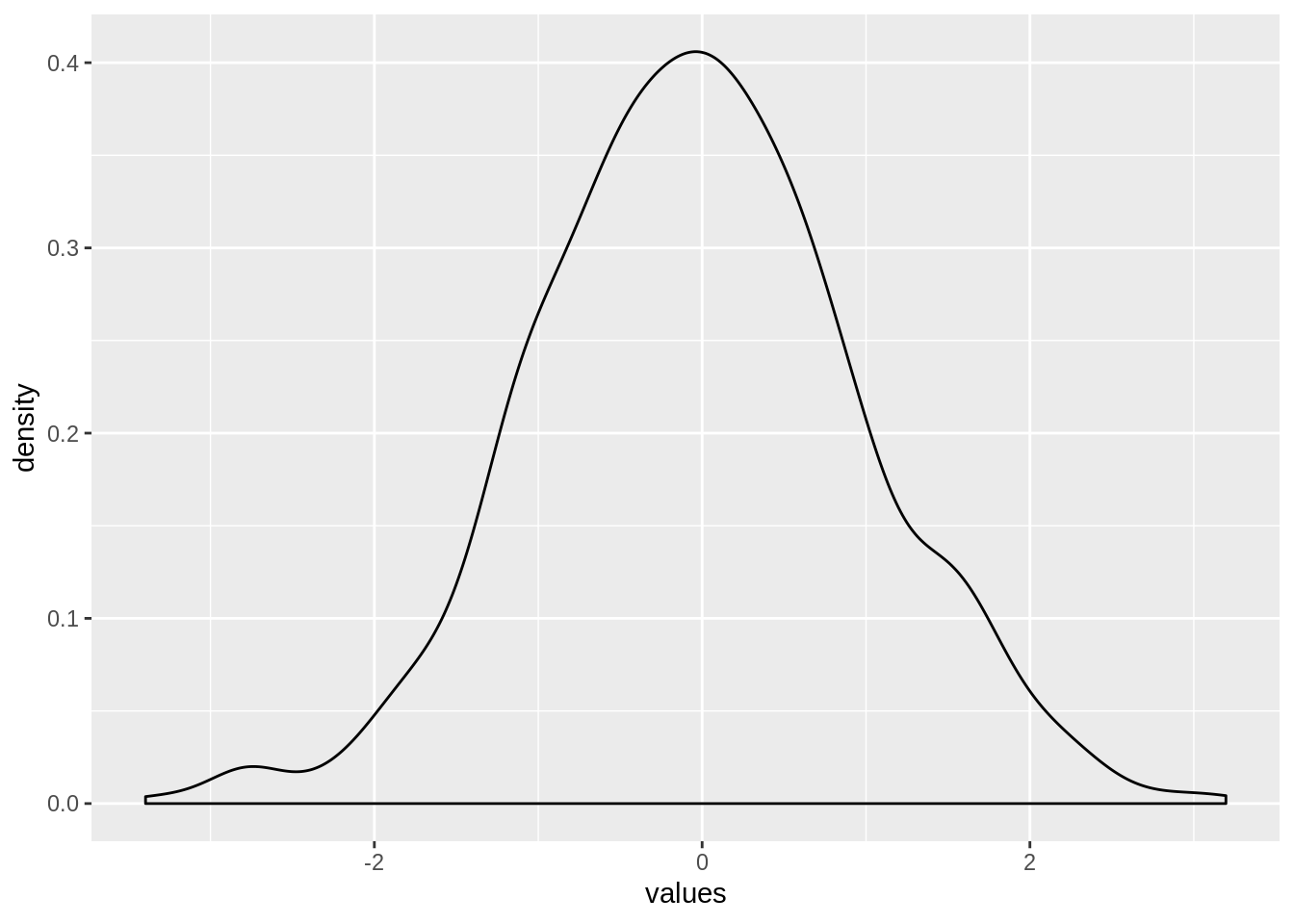

We can do a kernel density, which will return an object with a bunch of peices. One of these is y, which is the actual density value for each value of x that was used! So we can find the mode by querying x for the maxima in y!

density_estimate <- density(data_df$values)

mode_value <- density_estimate$x[which.max(density_estimate$y)]
mode_value

## [1] -0.04599328

Plot the density estimate with the mode location.

density_df <- data.frame(value = density_estimate$x, density = density_estimate$y)

ggplot(density_df, aes(x = value, y = density)) + geom_line() + geom_vline(xintercept = mode_value, color = "red")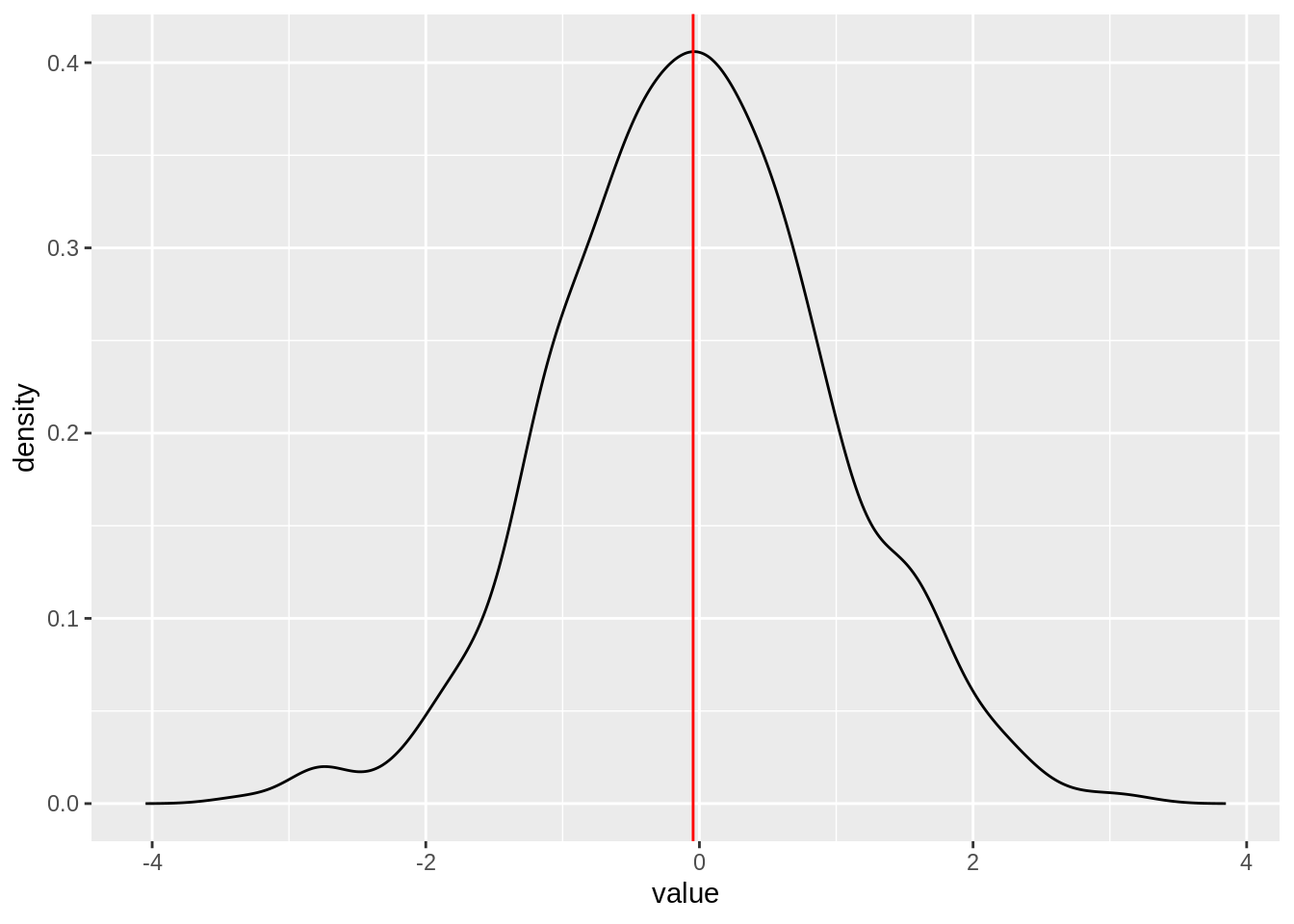

Python

Lets do something similar in Python. Start by generating a set of random values.

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
values = np.random.normal(size = 1000)
plt.hist(values)
plt.show()

And then use gaussian_kde to get a kernel estimator of the density, and then call the pdf method on the original values.

kernel = stats.gaussian_kde(values)
height = kernel.pdf(values)
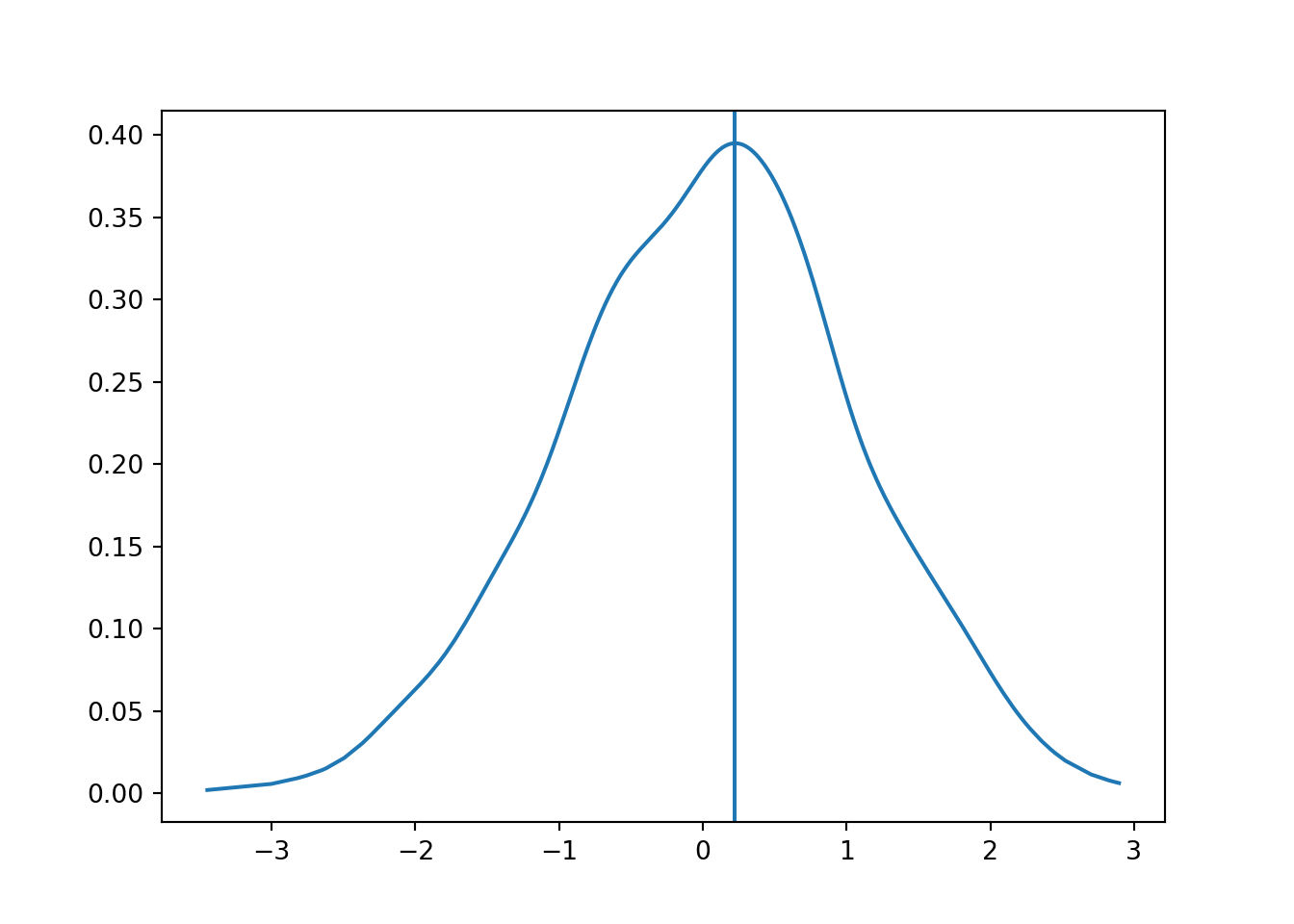
mode_value = values[np.argmax(height)]
print(mode_value)

## 0.22162730158854502

Plot to show indeed we have it right. Note we sort the values first so the PDF looks right.

values2 = np.sort(values.copy())
height2 = kernel.pdf(values2)
plt.clf()
plt.cla()
plt.close()
plt.plot(values2, height2)
plt.axvline(mode_value)
plt.show()